
This page is meant to be an introduction to the field of Quasicrystals in order to educate the interested reader on some basic concepts in this relatively new branch of Crystallography. The more advanced reader may proceed to other sites and sources on quasicrystals.
|
|
In classical crystallography a crystal is defined as a threedimensional periodic arrangement of atoms with translational periodicity along its three principal axes. Thus it is possible to obtain an infinitely extended crystal structure by aligning building blocks called unit-cells until the space is filled up. Normal crystal structures can be described by one of the 230 space groups, which describe the rotational and translational symmetry elements present in the structure. Diffraction patterns of these normal crystals therefore show crystallographic point symmetries (belonging to one of the 11 Laue-groups). In 1984, however, Shechtman, Blech, Gratias & Cahn published a paper which marked the discovery of quasicrystals. They showed electron diffraction patterns of an Al-Mn alloy with sharp reflections and 10-fold symmetry. The whole set of diffraction patterns revealed an icosahedral symmetry of the reciprocal space. Since then many stable and meta-stable quasicrystals were found. These are often binary or ternary intermetallic alloys with aluminium as one of the constituents. The icosahedral quasicrystals form one group and the polygonal quasicrystals another (8,10,12-fold symmetry). We can state that quasicrystals are materials with perfect long-range order, but with no three-dimensional translational periodicity. The former is manifested in the occurrence of sharp diffraction spots and the latter in the presence of a non-crystallographic rotational symmetry.
Since quasicrystals lost periodicity in at least one dimension it is not possible to describe them in 3D-space as easily as normal crystal structures. Thus it becomes more difficult to find mathematical formalisms for the interpretation and analysis of diffraction data. For normal crystals we can assign three integer values (Miller indices) to label the observable reflections. This is due to the three-dimensional translational periodicity of the structure. In order to assign integer indices to the diffraction intensities of quasicrystals, however, at least 5 linearly independent vectors are necessary. So we need 5 indices for polygonal quasicrystals and 6 indices for icosahedral quasicrystals. We can call them generalized Miller indices. The necessary n vectors span a nD-reciprocal space. Therefore there is also a nD-direct space in which a structure can be built that gives rise to a diffraction pattern as it is observed for quasicrystals. To put it simply we can say that in the higher-dimensional space we can describe a quasiperiodic structure as a periodic one. The actual quasiperiodic structure in the 3D-physical space can then be obtained by appropriate projection/section techniques. Thus it is enough to define a single unit cell of the nD-structure. The contents of that nD-unit cell consists of "hyperatoms" (occupation domains, ..) in analogy to the atoms in a normal unit cell. This enables us to describe the whole quasicrystal structure with a finite set of parameters. If we described it in 3D-space only, we needed thousands of atoms to obtain a representative volume segment of the whole structure as well as all parameters that go with it (eg. thousands of positions).
Example for a 1D-quasiperiodic sequence (Fibonacci chain)
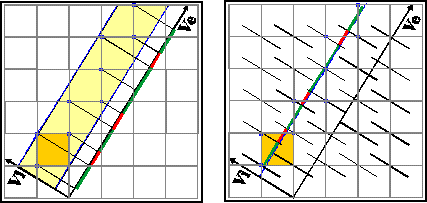 In order to elucidate this
concept with a simple example lets have a look at a 1D-"quasicrystal"
in form of a Fibonacci chain, which is a quasiperiodic sequence
of short (red) and long (green) segments. We embed this 1D-"quasicrystal"
in a 2D-"higher dimensional space" which in this case
has the form of a simple square lattice. One unit cell of the
higher-dimensional space is filled yellow. The axes show the
orientation of the two orthonormal subspaces Ve, Vi. The slope of
Ve with respect to the 2D-lattice has to be an irrational one. In
this case it is tau=1.618... The left image demonstrates the
projection method, where we have a strip of projection with
finite width. All points of the 2D-lattice inside this strip are
projected onto the external space Ve, thus giving the
quasiperiodic sequence (red,green..). The right image shows the
section method in which a hyperplane (here a 1D-line) that is
parallel to Ve cuts the higher-dimensional space. The occupation
domains that are attached to each of the lattice points (here:
bars) intersect with the hyperplane (here: line) thus producing
the same quasiperiodic sequence as in the left picture. These
occupation domains (here: bars) extend parallel to the internal
space Vi. We can generalize this to nD cases with n=5,6,.. In
that case the internal space would be (n-3)-dimensional and the
occupation domains would be two-dimensional (eg.polygons) or
three-dimensional (eg. polyhedra).
In order to elucidate this
concept with a simple example lets have a look at a 1D-"quasicrystal"
in form of a Fibonacci chain, which is a quasiperiodic sequence
of short (red) and long (green) segments. We embed this 1D-"quasicrystal"
in a 2D-"higher dimensional space" which in this case
has the form of a simple square lattice. One unit cell of the
higher-dimensional space is filled yellow. The axes show the
orientation of the two orthonormal subspaces Ve, Vi. The slope of
Ve with respect to the 2D-lattice has to be an irrational one. In
this case it is tau=1.618... The left image demonstrates the
projection method, where we have a strip of projection with
finite width. All points of the 2D-lattice inside this strip are
projected onto the external space Ve, thus giving the
quasiperiodic sequence (red,green..). The right image shows the
section method in which a hyperplane (here a 1D-line) that is
parallel to Ve cuts the higher-dimensional space. The occupation
domains that are attached to each of the lattice points (here:
bars) intersect with the hyperplane (here: line) thus producing
the same quasiperiodic sequence as in the left picture. These
occupation domains (here: bars) extend parallel to the internal
space Vi. We can generalize this to nD cases with n=5,6,.. In
that case the internal space would be (n-3)-dimensional and the
occupation domains would be two-dimensional (eg.polygons) or
three-dimensional (eg. polyhedra).
 Before quasicrystals were discovered in
1984 the british mathmatician Roger Penrose devised a way to
cover a plane in a nonperiodic fashion using two different types
of tiles. An example can be seen on the left. The tiles (rhombii)
are arranged in a way that they obey certain matching rules. An
equivalent tiling can be obtained for a 3D-arrangement. This is
called a 3D-Penrose Tiling, which is made up of rhombohedrons
instead of the rhombii. Such 2D and 3D-tilings have several
important properties, such as the selfsimilarity, which means
that any part of the tiling occurs again within a predictable
area (or volume). After the discovery of quasicrystals in 1984 a
close resemblance was noted between the icosahedral quasicrystal
and the 3D-Penrose pattern. By putting atoms at the vertices of a
3D-Penrose pattern one can obtain a Fourier Transform which
explains very well the diffraction patterns of the found Al-Mn
quasicrystal. In a similar way one can use 2D-Penrose Tilings (left)
to approximate a decagonal quasicrystal, which in a simple case
consists of two layers with local 5-fold symmetry, which are
rotated by 18 degrees so that the projection along the rotation
axis gives a 10-fold symmetry. As stated above it is also
possible to derive the vertices of such tilings using the nD-space
approach (n>3). In this case we can obtain such a tiling by a
projection of a nD periodic lattice (eg. hypercubic lattice).
Before quasicrystals were discovered in
1984 the british mathmatician Roger Penrose devised a way to
cover a plane in a nonperiodic fashion using two different types
of tiles. An example can be seen on the left. The tiles (rhombii)
are arranged in a way that they obey certain matching rules. An
equivalent tiling can be obtained for a 3D-arrangement. This is
called a 3D-Penrose Tiling, which is made up of rhombohedrons
instead of the rhombii. Such 2D and 3D-tilings have several
important properties, such as the selfsimilarity, which means
that any part of the tiling occurs again within a predictable
area (or volume). After the discovery of quasicrystals in 1984 a
close resemblance was noted between the icosahedral quasicrystal
and the 3D-Penrose pattern. By putting atoms at the vertices of a
3D-Penrose pattern one can obtain a Fourier Transform which
explains very well the diffraction patterns of the found Al-Mn
quasicrystal. In a similar way one can use 2D-Penrose Tilings (left)
to approximate a decagonal quasicrystal, which in a simple case
consists of two layers with local 5-fold symmetry, which are
rotated by 18 degrees so that the projection along the rotation
axis gives a 10-fold symmetry. As stated above it is also
possible to derive the vertices of such tilings using the nD-space
approach (n>3). In this case we can obtain such a tiling by a
projection of a nD periodic lattice (eg. hypercubic lattice).
In short, we can regard quasiperiodic tilings as frameworks that give quasicrystal structures when filled up with atoms in an appropriate way.
quasiperiodic in two dimensions (polygonal or dihedral quasicrystals)
There is one periodic direction perpendicular to the quasiperodic layers.
quasiperiodic in three dimensions, no periodic direction
new type (reported in Nature, Nov.2000)
The symmetry that determines the type of the quasicrystal is first seen in its diffraction pattern. Below some simulations of diffraction patterns are shown, which could represent either electron diffraction patterns or the zeroth layers of precession photographs (X-ray):
 octagonal QC |
 decagonal QC |
 dodecagonal QC |
Below there is a simulation for a Laue pattern (X-ray) from an icosahedral quasicrystal, whereby the x-ray beam is along one of the five-fold axes.
icosahedral QC
see also my Fourier transform gallery
below there is a link to a Java applet that calculates Fourier transforms from quasiperiodic tilings in analogy to diffraction patterns from two-dimensional quasicrystals
| octagonal
QC: V-Ni-Si |
decagonal QC:
Al-TM (TM=Ir,Pd,Pt,Os,Ru,Rh,Mn,Fe,Co,Ni,Cr)
|
| dodecagonal
QC: Cr-Ni |
icosahedral QC:
Al-Mn |
| new type: Cd-Yb * stable binary quasicrystal |
* stable phases exist
| selected
area electron diffraction (SAED) |
obtain reciprocal space information (symmetry, point group) |
| convergent beam electron diffraction (CBED) | determination of the point group & space group |
| high
resolution transmission electron microscopy
(HRTEM) |
real structure information
(below decagonal Al-Mn-Pd)  |
| X-ray diffraction techniques | Film methods: Laue, Precession,
Debye-Sherrer Quantitative measurement: Powder diffractometer, Four-circle diffractometer |
| neutron diffraction | obtain partial structure factors to assist structure refinement |
| Kossel technique | (see KOQUA2.2) |
There are basically two different methods for solving the structure of quasicrystals. The first one is a 3D method, where information obtained from HRTEM images and known approximant structures is combined to obtain a realistic structure model.
The second one is the so-called nD structure analysis (n>3), where the structure is modeled in terms of the contents of the nD unit cells, i.e. the occupation domains. In contrast to the 3D method this is a quantitative analysis, which allows to calculate diffraction patterns and to refine a variety of parameters by the least-squares method. It therefore allows us to use all mathematical tools that have been applied in the analysis of conventional crystals, however, extended to the nD space. This technique may include the steps listed below, assuming the application of the nD-maximum entropy method as used by YAMAMOTO et al.
Step 1 - information on the three-dimensional structure
HRTEM images should be taken to obtain as much structural
information as possible on the actual three-dimensional structure.
For polygonal quasicrystals this means in particular the
clarification of the cluster arrangement (in case there are basic
clusters that form the whole structure). For icosahedral
quasicrystals it is not possible as easily to determine cluster
positions, since the high-resolution image shows only the
projected structure along some direction. Information on the
third spatial coordinate is therefore lost and possibly present
clusters cannot accurately be associated with x, y and z-coordinates.
The HRTEM images have a limited resolution in direct space so
that the actual atom arrangement (distinction between atom
species) within one cluster cannot be determined. Therefore an
approximant structure can be helpful in giving a possible atom
arrangement for some clusters, which can then be introduced into
the structure model. An X-ray structure analysis for the
approximant is in most cases straightforward and might even have
been done before, so that already published data might be readily
available.
This step 1 corresponds to the above mentioned first
structure solution procedure.
Step 2 - location of occupation domains
The basis for the quasicrystal structure analysis is a single (quasi)crystal
X-ray data set, usually taken on a four-circle diffractometer. (In
future, however, imaging plate techniques might gain importance,
since they allow rapid simultaneous measurements of many
reflections including diffuse scattering intensities) The first
thing to do with the measured X-ray data is to determine the
exact location of the occupation domains. This can be done by
using the nD Patterson method, which does not require any
structure model, since only the square amplitudes of the
structure factors go into the calculation.
Step 3 - nD starting model
The information from the first thwo steps is then combined to
obtain a first rough nD structure model. This consists of
a number of occupation domains at their determined locations. The
occupation domains have to be constructed in such a way that by
applying the section method the observed cluster arrangement is
obtained, as well as the atomic decoration of the clusters as
suggested by a known approximant structure.
Step 4 - MEM (maximum entropy method)
The starting model will then be refined, in order to obtain the
phases of some strongest reflections, which is necessary for the
MEM calculations. After performing the MEM calculations internal
space MEM maps have to be plotted. These MEM maps provide
information on the presence of possibly new (additional)
occupation domains. Furthermore they show in more detail the size
and shape of the occupation domains and the peak heights give
hints on the distribution of transition metal atoms.
Step 5 - structure model modification
The information obtained from the MEM maps is then used for the
modification of the nD structure model (i.e. the
occupation domains). If necessary newly found ODs have to be
constructed. The most difficult part is the distribution of atom
species among the occupation domains. This is despite the
findings in the MEM maps a trial and error procedure, due to the
frequently occurring mixed occupancies. Key indicators for a
structure model to be reasonable is the calculated point density
and the calculated chemical composition.
Step 6 - refinement
The constructed structure model is then refined by means of the
least-squares method. The necessity of further model
modifications might arise so that steps 5 and 6
have to be repeated until a satisfactory structure solution is
found. The refinement should include all necessary positional,
occupational and thermal parameters.
Step 7 - structure plots
After obtaining the final structure model, several structure
projections need to be drawn in order to elucidate the resulting
structure. Since the section method provides all atom positions
in x, y and z coordinates, individual clusters can be cut out (using
suitable software, such as XRSV) and plotted separately, in order to
show more clearly the local structure in the clusters.
For the stable quasicrystals it is possible to observe the growth morphology. Decagonal quasicrystals, such as Al-Ni-Co or Al-Mn-Pd grow as distinguished decaprismatic columns. (ten prism faces with the 10-fold axis as rotation axis).The icosahedral quasicrystals grow with triacontahedral shape (Al-Cu-Li) or with pentagon - dodecahedral morphology (face-centered icosahedral Al-Cu-Fe). The Triacontahedron exhibits 30 rhombic faces perpendicular to the 2-fold axes and the Pentagon-Dodecahedron 12 faces perpendicular to the 5-fold axes.
For some icosahedral shapes see my Polyhedra applet and choose an icosahedral point group (235 or m-3-5).
Comparison between Incommensurately Modulated Structures and Quasicrystalline Structures.
common characteristics
-diffraction patterns with sharp diffraction spots (Bragg
reflections)
-translational symmetry neither in direct nor in reciprocal space
-embedding in a nD-reciprocal lattice gives a periodic nD-structure
differences
IMS:
-main and satellite reflections
-average structure
-crystallographic point symmetry
QCS:
-one kind of reflections only
-no average structure
-non-crystallographic point symmetry
-special cuts of the nD-supercrystal always give IMS
This glossary contains explanations of some keywords that frequently occur in papers related to quasicrystals and is meant as help for the interested reader who is not familiar with these terms.
Amman grid
An Amman grid results from a special decoration of Penrose
tilings, whereby the basic tiles are decorated with line segments.
In its appearance it is similar to a quasiperiodic multigrid as
used in the generalized dual method (GDM).
approximant
Crystalline approximants are structures which are periodic, but
which are very similar to quasicrystals. Usually these
approximants have very large unit cells. They play an important
role in solving quasicrystal structures. They are related to
quasicrystals by a phason strain or a rotation in nD space
(both are equivalent).
Bergman cluster
Icosahedral cluster for Frank-Kasper phases consisting of 117
atoms. A central atom (1) is enclosed by several shells of atoms,
that are placed at the vertices of some polyhedra of increasing
size. In successive order these are: icosahedron (12) + pentagon
dodecahedron (20) + icosahedron (12) + soccer ball (60) +
icosahedron (12) = 117 atoms.
cluster model
Structure modeling technique in which some kind of cluster is
placed at the vertex positions of a 2D or 3D tiling. This is
contrary to a decoration. The clusters are assumed to be
columnar for polygonal quasicrystals. For icosahedral
quasicrystals the clusters reflect the icosahedral symmetry, e.g.
the Mackay icosahedron or the Bergman cluster.
composite crystal
General form of IMS, which consists of two or more
interacting modulated substructures.
decoration
Structure modeling technique in which the basic tiles of a 2D or
3D tiling are filled up ("decorated ") with atoms to
obtain a quasiperiodic structure. Equivalent tiles have the same
decoration, which is not the case in the cluster model.
dual method (DM)
Method which transforms enclosed areas formed by a multigrid into
vertices of a quasiperiodic (or periodic) tiling. For a n-fold
rotational symmetry the multigrid consists of n sets of
parallel lines with equidistant spacing, which are rotated
against each other by 360/n.
embedding
Description of a 3D-quasiperiodic structure in terms of a nD-periodic
structure (n>3)
external space
The 3D-subspace of the nD-space, which corresponds to our
real 3D physical space.(also parallel space, VE, Vpar)
Fibonacci chain
A quasiperiodic sequence of short and long segments S and L. This
can be obtained by iteratively replacing SL and L LS. (e.g.:
LSLLSLSLLSLLS...). It is a 1D-analogon to quasicrystals.
generalized dual method (GDM)
See dual method (DM). The difference to the DM lies in the
use of quasiperiodic grids, i.e. sets of parallel lines with
spacings similar to the Fibonacci sequence.
golden ratio
tau=1/2(1+SQRT(5))=1.618... (also golden mean). In the Fibonacci
chain "tau" gives the ratio of lengths between the
short and long segments. It also relates to the slope of the
external space (VE) towards the higher dimensional-lattice, which
has to be irrational in order to insure that the projection
method and the section method produce quasiperiodic arrangements.
higher-dimensional space
Space with dimensions >3 that is used for a fictitious
periodic lattice or structure from which quasiperiodic tilings or
structures can be derived. This nD-space is usually split
into two subspaces, which are perpendicular (orthonormal) to each
other. These are the 3D-external and the (n-3)D-internal
space. (VE, VI)
honeycomb tiling
Dual of the Stampfli tiling. The double honeycomb tiling
is formed by two hexagonal nets, which are rotated against each
other by 30.
HRTEM (high resolution transmission
electron microscopy)
Powerful tool for elucidating the real structure. It is of
special importance for polygonal quasicrystals, since it reveals
the arrangement of columnar clusters in when viewing the
structure along its unique n-fold axis.
icosahedral glass model
Icosahedral clusters are randomly aggregated within certain rules
concerning vertex-, edge- and face-sharing and the preservation
of bond-orientational order.
inflation/deflation method (IDM)
Generation of quasiperiodic tilings, by putting several primitive
tiles according to local matching rules.
internal space
The (n-3)D-subspace of the nD-space, which forms
the complementary space to the external space.(also perpendicular
space, VI, Vperp)
IMS
see modulated structure.
Local Isomorphism
Local isomorphism (LI) is a key feature in generating and
classifying quasilattices. For a fixed orientational symmetry,
fixed set of basic tiles and fixed frequency with which these
tiles occur there are an infinite number of inequivalent
quasilattices. Therefore the new concept of local isomorphism is
introduced, which allows to group the inequivalent quasilattices
into equivalence classes (LI classes). Inequivalent quasilattices
are locally isomorphic if every finite arrangement of tiles in
each is found in the others.
Mackay icosahedron
54 atom cluster with icosahedral symmetry consisting of three
successive shells. These are a regular small icosahdron (Al) +
large icosahedron (TM) + icosidodecahedron (Al) .
MEM map
A MEM map as used here is an electron density map calculated by
the maximum entropy method. The key feature is a very high
smoothness of the map without series truncation errors as in the
Fourier map. Here we distinguish between internal and external
space MEM maps. The former shows the occupation domains and the
latter corresponds to the real space structure.
maximum entropy method (MEM)
Information theory shows that the best electron density is the
one that maximizes the entropy S subject to 2,
which are constraints in the form of observed intensity data. The
maximization is therefore achieved by minimizing 2. In the
nD-MEM the nD unit cell is pixelized by a nD
grid. If there are m intervals along each basis vector we
have therefore mn grid points. For each grid point the
electron density is calculated, whereby the information of the
whole unit cell in Fourier space is used (mn structure
factors). In the case of a 5D space with 20 intervals 205=3.200.000
structure factors are calculated, which results in a high
resolution in Fourier space and consequently in direct space.
modulated structure
A state between normal crystals and quasicrystals. The structure
is modulated, whereby the period of the modulations can be
incommensurate with the translation period of the lattice (IMS=incommensurately
modulated structures). Usually described in 4-6D-space, depending
on the number of dimensions with a modulation.,
multigrid
Set of grids which are rotated by an angle, which is defined by
the desired symmetry. A grid is a set of parallel lines, which
are spaced equidistantly (periodic grid) or in a Fibonacci chain-like
fashion (quasiperiodic grid). The former is used in the Dual
Method and the latter in the Generalized Dual Method.
occupation domain
Also acceptance domain or hyperatom. Occupation domains (OD) can
be regarded as "superatoms" in a fictitious higher-dimensional
unit cell. These ODs are two-dimensional for polygonal
quasicrystals and three-dimensional for icosahedral quasicrystals.
Using the projection or section method these ODs create the atoms
in the real space. Hereby different parts of the ODs can create
different types of atoms, which means that they usually are not
homogeneous but have a chemical fine-structure. The essential
part in the refinement of a quasicrystal structure is to find the
correct position, size, shape and chemical composition of the ODs.
Their shapes are restricted by the site symmetry of their
position, from which often highly symmetrical shapes arise.
Penrose tiling
Two-dimensional covering of the plane in a quasiperiodic fashion
using two types of tiles (skinny & fat rhombii). There are
also other Penrose Tilings, such as the Generalized Penrose
Tilings or the Pentagonal Penrose Tiling, which is made up of
pentagons instead of rhombii.
phason strain
We distinguish between the linear and the random phason strain.
The linear phason strain is equivalent to a rotation in nD-space
(n>3). The phason strain lets the internal space (VI)
unchanged, but leads to a rearrangement of tiles (so-called
phason flips) in the real space (VE) and to a shifting of the
reflection spot positions. The random phason strain corresponds
to a random shift of the ODs along VI and can be accounted for by
introducing an additional temperature factor for the internal
space.
point group
Rotational part of symmetry elements without consideration of
translations. There are 32 3D crystallographic point groups, of
which 11 include inversion symmetry (Laue groups).
projection method
Method which projects points of a fictitious higher-dimensional
lattice or structure into the real physical space (3D).
quasicrystal
Material which shows diffraction patterns with rotational
symmetries, that are "forbidden" by classical
crystallography. The structure of quasicrystals comprises of
atoms that are arranged in a nonperiodic fashion. Quasicrystal
structures show long-range order, but no translational
periodicity. Quasicrystal structures can be approximated by
filling an appropriate quasiperiodic tiling with atoms.
random tiling
Tiling in which the basic tiles of a quasiperiodic tiling (2D/3D)
are put together in a random fashion, thus neglecting local
matching rules. The long-range orientational order, however
remains due to the shape of the tiles. The diffraction patterns
are therefore similar to the ones from ideal quasiperiodic
tilings.
reciprocal space
The reciprocal space (also Fourier space) is a concept in
crystallography which proved invaluable for the interpretation of
(X-ray) diffraction patterns. While the atoms are at positions of
a "direct" lattice the reflections arising from certain
atom planes are at positions of the "reciprocal"
lattice. Between both lattices exists a simple inverse-relationship.
If the direct lattice is known we can thus easily derive the
possible positions of reflections, whereas the Fourier transform
of its electron density (structure) gives us the corresponding
intensities. Among others this can be used for simulating
diffraction patterns in order to compare them with experimentally
obtained ones.
section method
Generalized projection method. The section method uses occupation
domains in the higher-dimensional unit cell. All atom positions
in 3D are then obtained from the intersection of the occupation
domains with the 3D external space.
space groups
The 230 symmetry groups with rotational and translational
symmetry elements, by which normal 3D-structures are
characterized. The concept of space groups is now extended to the
nD space (n>3), in order to include the space groups of
quasicrystals.
Stampfli tiling
Dual of the double honeycomb tiling. It is a tiling with
dodecagonal symmetry consisting of triangles, squares and skinny
rhombii.
superspace groups
In extending crystallography, which defines 230 different 3D-space
groups to a higher-dimensional crystallography, superspace groups
were introduced to describe modulated structures. They are not
identical with the nD space groups for quasicrystals,
because of their finer classification.
| T.Fujiwara, T.Ogawa:
Quasicrystals Springer Verlag, 1990 |
| D.P.DiVincenzo, P.J.Steinhardt: Quasicrystals: The State of the Art Singapore: World Scientific, 1991 |
| C.Janot: Quasicrystals - A Primer Clarendon Press, Oxford, 1992 |
| K.H.Kuo, S.Takeuchi:
Quasicrystals and Imperfectly ordered Crystals Trans Tech Publications, 1994 |
| M.Senechal:
Quasicrystals and Geometry Cambridge University Press, 1995 |
| G.Chapuis, W.Paciorek: Aperiodic '94 Singapore: World Scientific, 1995 |
| Ch.Janot, R.Mosseri: Quasicrystals: Proceedings of the 5th International Conference Singapore: World Scientific, 1995 |
| F.Axel: Beyond Quasicrystals New York: Springer Verlag, 1995 |
| S.Takeuchi, T.Fujiwara: Quasicrystals: Proceedings of the 6th International Conference Singapore: World Scientific, 1998 |
| C.Beeli, W.Steurer: Proceedings of the "Workshop on Quasicrystal Structure Analysis", ( a satellite meeting to the "7th International Conference on Quasicrystals", September 24th/25th 1999, Stuttgart, Germany. Zeitschrift für Kristallographie Vol. 215 (2000) issue 10, ISSN 0044-2968 Oldenbourg Wissenschaftsverlag, D-81671 Muenchen, Germany |
|
A.I. Goldman, D.J. Sordelet, P.A.
Thiel, J.M. Dubois (eds):
New horizons in
quasicrystals. Research and Applications.
World Scientific, Singapore
(1997)
|
|
Z. Stadnik (ed.):
Physical properties of
Quasicrystals
Springer, Heidelberg-New York
(1999)
|
|
E. Belin-Ferre, C. Berger, M.
Quiquandon, A. Sadoc:
Quasicrystals. Current Topics.
World Scientific, Singapore
(2000)
|
|
F. Axel, F. Denoyer, J.P. Gazeau
(eds):
From quasicrystals to more
complex systems
Springer, Heidelberg-New York
(2000)
|
|
F. Gähler, P. Kramer, H.-R.
Trebin, K. Urban (eds):
Proceedings of the 7th
International Conference on Quasicrystals
Mater. Sci. Eng. A 294-296
(2000) 1-912.
|
|
Steurer, W. and Haibach,
T.:
Reciprocal space images of aperiodic crystals. In: International Tables for Crystallography. Vol. B, Ed. U. Shmueli, Luwer Academic Publishers: Dordrecht. (2001) 486-518. |
| Walter Steurer: The Structure of Quasicrystals Zeit.f.Krist.190, 1990 |
| A.I.Goldman, R.F.Kelton: Quasicrystals and Crystalline Approximants Rev.of Mod.Phys., Vol 65, No.1, 1993 |
| Akiji Yamamoto: Crystallography of Quasiperiodic Crystals Acta.Cryst.A52, 1996, 509-560 |
| QuaRef | QuasiCrystal Reflection Generator (Windows 95/98/2000/NT) NEW! |
| QuasiTiler 3.0 | quasiperiodic tilings by the projection method |
| Tiling | quasiperiodic tilings by the dual method (DOS,Windows) |
| Koqua2.0 | Laue- and Kossel-diffraction patterns (DOS,Windows) |
| VSV | Vector Space Viewer, visualization in Vi & Ve (DOS,Windows) |
| Polyhedra | draws polyhedra with icosahedral symmetry (DOS,Windows) |
| Fourier Transform | similar to optical diffraction patterns (DOS,Windows) |
| QREFGEN | quasicrystal reflection generator (DOS,Windows95) |
| DECA-ZONAX1.0 | zone axis patters for decagonal phases (DOS,Windows) |
| JAVA applets | Stereogram, Lauegram, JTiling, JFourier3 (Java) |
| Japan: | Dr.Akiji Yamamoto (NIRIM, Tsukuba) |
| Switzerland: | Prof. Walter Steurer (ETH, Zuerich) |
| Spain: | Elcoro, Perez-Mato, Madariaga (Pamplona, Bilbao) |
| Logo for the 6-th International Conference on Quasicrystals |
The book "Quasicrystals: Proceedings of the 6th International Conference" uses the design of my poster (right) for the cover illustration (left), although they don't mention that.
